
Image credit: NASA's Earth Observatory
Such details have already been dealt with by experts ages ago. Their efforts have led to a range of definitions which are useful with different purposes. This document aims to provide a short overview of the most commonly used terms. As a starting point, we need to take a few steps backward - or actually many steps backward, namely into outer space ...

The geometrical shape of such a rotational ellipsoid can be uniquely defined in terms of two parameters, such as the semi-major and semi-minor axes. As more observations are collected from more advanced observing systems and modelling techniques develop, these parameters are getting refined at regular intervals and for various purposes. For this reason, several "realisations" of the rotational ellipsoid exists. Some of the most popular ones are listed in the table below.
| Reference ellipsoid | Semi-major axis | Semi-minor axis |
|---|---|---|
| Geodetic Reference System of 1980 (GRS80) | 6 378 137.0 m | 6 356 752.3 m |
| World Geodetic System of 1984 (WGS84) | 6 378 137.0 m | 6 356 752.3 m |
| TOPEX/Poseidon | 6 378 136.3 m | 6 356 751.6 m |
The ellipsoidal surface forms a standard reference surface in space, relative to which we refer geospatial observations. It is of great practical importance since it is easy to use and defined from a purely mathematical perspective. Once the parameters are defined, it does not change in time unless we choose to update the parameters. In contrast, sea level varies constantly and requires constant maintaince in order to give physical meaning. Futhermore, as the use of GPS has become standard instrumentation for basically all geopspatial observations and the World Geodetic System of 1984 (WGS84) forms the basis for this observing system, essentially all geospatial data have an associated set of ellipsoidal coordinates.
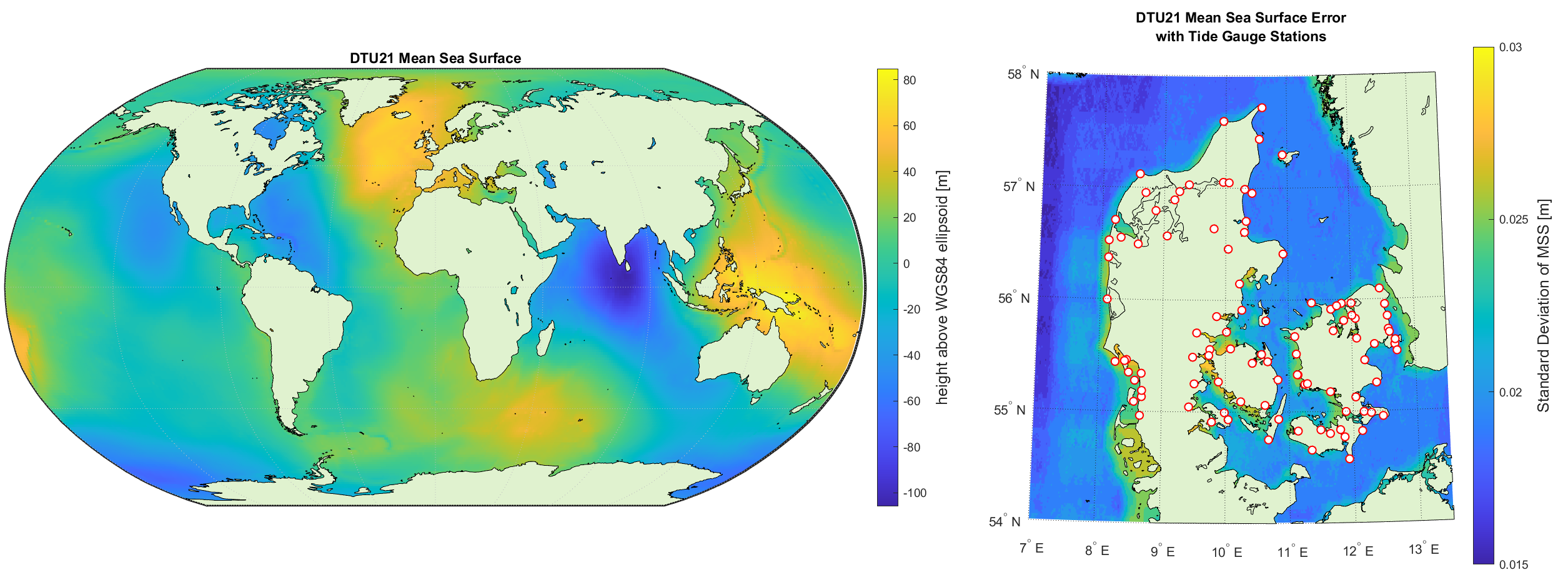
The ocean surface can be measured on a global scale from satellite altimetry. Essentially, the satellite measures its own distance from the ocean surface. The position of the satellite is derived from an onboard GPS system, which makes it possible to specify the sea surface in terms of ellipsoidal coordinates. One matter of complication is that the return signal from the distance measurement does not originate from a single point on the ocean surface, but instead an average distance to some surface area. The size of the area is known as the "footprint" of the satellite and thus determines the spatial resolution of the observations. Generally speaking, satellites with a large footprint, i.e. low spatial resolution, repeat their orbits from about 10 days, resulting in a high temporal resolution, while satellites with a small footprint, i.e. high spatial resolution, may take more than one year before they repeat their orbits. Satellite altimetry has been a revolutionary measurement method allowing for the determination of MSL on a nearly global scale at an accuracy of 1 to 2 cm. However, it does contain some limitations. First of all, the orbit geometry means that the polar regions are not covered by this technique. Second, the footprint of the measurements limit its use in coastal regions, where the signal is easily obscured. The above figure to the right illustrates how the associated condifence in MSL from satellite altimetry decreases along the coastal regions in Denmark.
In the coastal areas, we therefore use another important measurement method: tide gaugues. These are essentially permanent stations in the coastal water that continously measure the change in water level. Whereas satellites are far away, i.e. have a large footprint, and constantly move, tide gauges represent "point" measurements at a fixed location. One important and often cumbersome aspect of using tide gauges is to link the instrument position to a monument of known position on land in order to provide a reference to an "absolute" height, i.e. the reference ellipsoid. As the relative position of the monument and tide gauge may change in time, this link must be checked at regular time intervals. This link is typically provided using some sort of levelling.
Below is a figure illustrating the basic concepts of the two measurement methods.
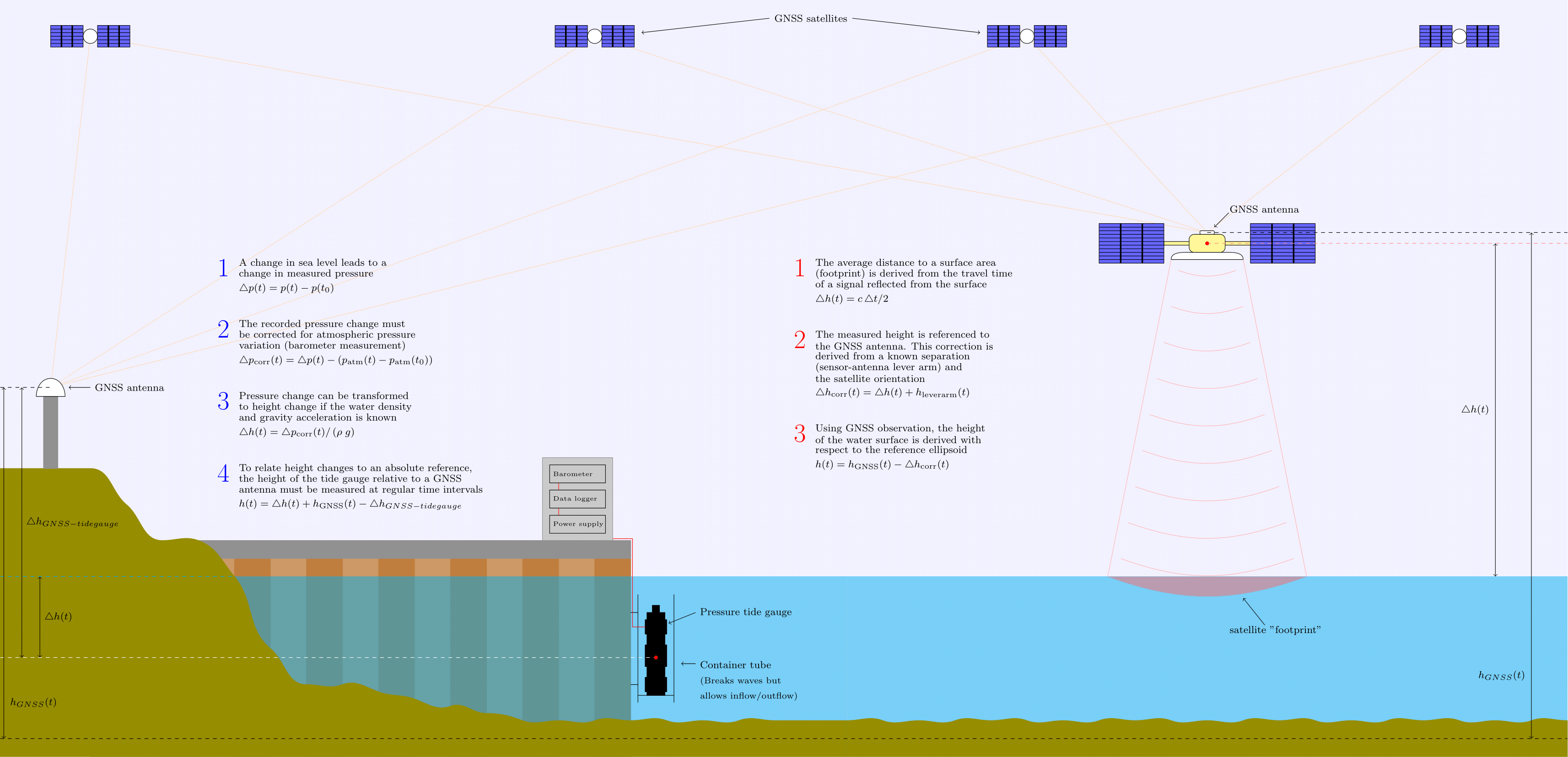
The temporal continuity and resolution is important to derive MSL. Long time series are essential to provide useful observations, ideally ranging 18.6 years in order to fully account for the complete tidal period of the lunar cycle. Other measurement methods from e.g. shipborne surveys are also used for observing the sea surface. Typically these methods are not suitable for long-time monitoring, meaning that temporal averaging is not possible and alternative modelling approaches must be employed in order to derive the MSL.
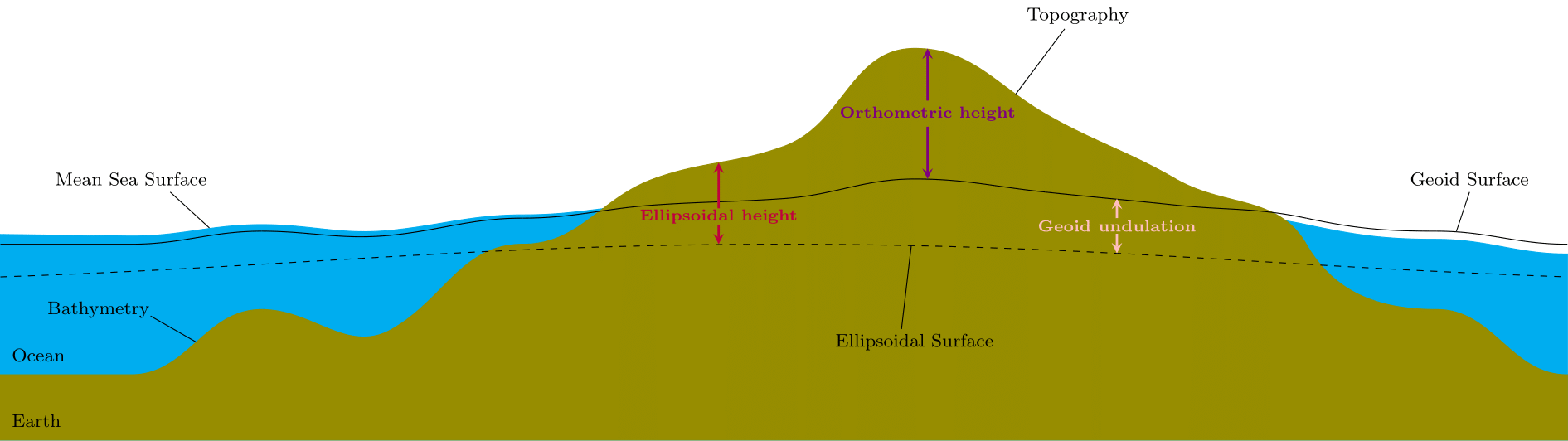
Table with overview of surfaces and applications relevant to each surface